So finden Sie die Höhe eines schrägen Dreiecks mit Fläche

Die Höhe eines Dreiecks können auf unterschiedliche Weise gefunden werden, je nach Art des Dreiecks und der gemessenen Informationen. Rechteckige Dreiecke, die einen Winkel von 90 Grad einschließen, lassen sich am einfachsten mit dem Satz des Pythagoras (wenn die Längen beider Seiten bekannt sind) oder der Flächenformel (wenn Fläche und Basis bekannt sind) messen. Gleichseitige Dreiecke, bei denen alle Seiten gleich lang sind, und gleichschenklige Dreiecke, bei denen drei Seiten gleich lang sind, können in zwei Hälften geschnitten werden, wodurch zwei Dreiecke entstehen. Aber schräge Dreiecke, deren Innenwinkel 90 Grad beträgt, sind härter und erfordern Trigonometrie um ihre Größe herauszufinden. Dann berechnen Sie die Höhe von an schräges Dreieck mit der Flächenformel.

1. ttttZeichne zuerst das Dreieck und benennen die Seiten und die bekannten Werte.

• A, B und C sind die Winkel.
• a, b, c sind die Seiten
• h ist die Höhe

In diesem Beispiel A = 60 Grad und b = 5.

2. Geben Sie die Flächenformel ein:

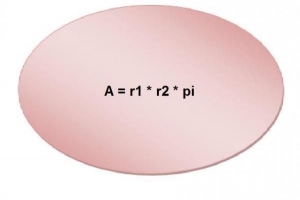
• A = 1/2 bh (A = Fläche, b = Grundfläche, h = Höhe)

Alle Werte sind nicht erforderlich, aber die Formel hilft dabei, alles richtig auszurichten.

3. Suchen Sie nach der Seite neben der Basis. [Seite b = 5]

4. Finden Sie die Winkel neben der Basis und die Seite in Schritt 3. Wenn Sie es nicht wissen, hilft Ihnen ein Winkelmesser, wenn den Winkel messen. [Winkel A = 60]

5. Geben Sie die Höhenformel, das ist die Seite neben der Basis, multipliziert mit dem Sinus des Winkels neben der Seite. [h = 5sin60]

6. Führen Sie Berechnungen durch, um die Höhe zu finden. [h = 5 x 0.87 = 4,33]

• Die Basis kann eine beliebige Seite des Dreiecks sein.
• Die Methode der Trigonometrie (mit Sinus) kann auch auf Dreiecke angewendet werden.
• Die drei Winkel eines Dreiecks müssen zusammen 180 Grad ergeben.